Coverage-based Greybox Fuzzing as Markov Chain

1 介绍

现有fuzzer最主要的挑战是：许多fuzz执行少数相同路径。举个栗子，fuzzing一张有效的图片文件，那么变异后的图片有90%的可能性执行拒绝无效图片文件的路径$\pi$。fuzzing一张无效的图片文件，有99.999%的概率变异之后的文件执行相同的路径$\pi$。我们称路径$\pi$为high-frequency路径。

所以本文工作提出一些策略来帮助在相同的fuzz次数下探索low-frequency路径。实验结果表明我们的AFL工具在GUN binutils中发现9个漏洞，他们被在US National漏洞数据库中列为CVEs（Common Vulnerabilities & Exposures，常见的漏洞和风险)。AFLFAST发现6个CVEs的速度是AFL的14倍，发现3个在8次运行24小时的fuzz中AFL没发现的CVEs。

AFLFast的核心思想（似乎？）是对初始化的种子非常低的能量，每当种子被选择后（TM看不懂。。）主要实现了一个power schedule，慢慢看吧。。

AFL实现的power schedule总是给予高能量（high energy）。给初始化种子大量的能量能够帮助发现更多近邻，这些近邻执行low-frequency路径。举个栗子，fuzz一张有效的图来生成更多有效的图make sense。而且赋值给这些近邻也很make sense。但是执行一段时间后，发现了更多种子，这些种子会执行high-frequency路径，导致若最新的种子是无效图片文件，生成合法图片文件的概率显著降低。

而AFLFAST给high-frequency路径低能量，给low-frequency路径高能量。为了估计fuzzer执行路径$i$的概率，AFLFAST使用最大似然估计$\hat{p}_i=f(i)/n$，$f(i)$是fuzz执行$i$的次数，$n$是fuzz生成所有测试用例经过路径的总数。

同时发现power schedule和search strategies仅仅改变了AFL的效率（单位时间内发现的路径数），并没改变性能（发现路径的数量）。也就是说在发现漏洞的能力上和AFL相同，只是发现的更快。

本文以KLEE这个符号执行器作为baseline进行漏洞检测比较。在KLEE-benchmark上9个error中的6个error，KLEE发现的速度比AFLFAST快，但是AFLFAST找到了5个新的bug。考虑代码覆盖率，AFLFAST比KLEE稍好，AFLFAST平均覆盖82%的代码，KLEE平均覆盖78%。

本文贡献：

1. Markov Chain Model. 把基于覆盖的灰盒fuzzing建模成一个有状态空间的Markov chian的系统探索模型
2. Power Schedule. 提高较少执行路径执行的可能性

3. Search Strategies.

4. Comparison to Symbolic Execution.

5. Tool. AFLFAST

2 背景

2.1 CGF(Coverage-based Greybox Fuzzing)

cur_location = <COMPILE_TIME_RANDOM>;
shared_mem[cur_location ^ prev_location]++;
prev_location = cur_locationi >> 1;

左移1位是为了区分基本块A和B的顺序的影响。另ID(A) ^ (ID(B)>>1) ≠ (ID(A)>>1) ^ ID(B)。

Fuzzing stages. AFL对种子输入进行fuzz，随机选择一系列的变异策略并应用到种子输入的随机位置。在确定性变异策略阶段，AFL在输入的每个字节上进行某些变异策略。我们可以认为首次被选到的种子输入有很高的能量。

Binary instrumentation.

Modifications. 本工作只关注CHOOSENEXT实现的搜索策略和ASSIGNENERGY实现的power schedules策略。

2.2 马尔科夫链

一个Markov chain是一个随机变量的序列$\{X_0, X_1, \dots, X_n\}$，$X_i$表示在时间$i$时的状态，状态的集合为$S=\{1, 2, \dots, N\}, N\in\mathbb{N}, X_i\in S$。马尔科夫链以状态$i$为初始状态的初始分布为$\mathbb{P}(X_0=i)$。

概率矩阵为$\mathbf{P}=(p_{ij})$，若$|S|=N$，那么$\mathbf{P}$为$N\times N$的矩阵，每行的和为1。其中$p_{ij}=\mathbb{P}(X_{t+1}=j|X_t=i)$。

另$\mathbb{\pi}$表示马尔科夫链的stationary distribution（这是固有分布我终于看懂了哈哈哈哈哈哈哈哈），那么$\forall j\in S$满足：

$$0\leq \pi_j\leq 1 \\ 1 = \sum_{i\in S}\pi_i \\ \pi_j = \sum_{i\in S}\pi_ip_{ij}$$

3 马尔科夫链模型

3.1 Coverage-based Fuzzing as Markov Chain

Time-in homogeneous model. 假如fuzzer的初始化种子输入$t_0$执行路径0，输入$t_i$执行路径$i$之后马上探索到路径$i+1$。那么转换概率$p_{ij}$定义为生成的输入执行了路径$j$若它是由上一个输入$t_i$执行了路径$i$变异得到的。但是$p_{ij}$依赖于状态$i$到达的路径。假如一个输入$t_i’$也经过了路径$i$，那么$p_{ij}$执行路径$j$的概率会很不一样。也就是说这个马尔科夫链不是时间同构的。

Time-homogeneous model. 给定种子$T$，$S^+$表示由$T$执行到的路径集合，$S^-\nsubseteq S^+$表示由fuzzer变异得到的输入执行到的路径。那么马尔科夫链的状态集合就是

$$S = S^+\cup S^-$$

状态矩阵$\mathbf{P}=(p_{ij})$可以表示为：若$i\in S^+$，$p_{ij}$就是由种子$t_i$变异后的输入执行路径$j$的概率；否则若$i\in S^-$，那么$p_{ii}=1-\sum_{t_j\in T}p_{ji}$，其中$p_{ij}=p_{ji}, \forall\ t_j\in T$。这里有俩假设：

1. 从种子$t_i$变异得到输入执行路径$j$与从种子$t_j$执行路径$i$相似
2. $i\in S^-$没有其他的未发现邻居

根据大数定律，当执行步数$N$趋向于无穷大时，执行状态$i$的比例会趋向于固有分布$\pi_i$。

我们称$\pi$的一个$high-density\ region$是一个路径的近邻$I$满足$\mu_{i\in I}(\pi_i)\gt\mu_{t_j\in T}(\pi_j)$，其中$\mu$是算术平均。$low-density\ region$同理。路径$i$和$j$在同个邻居中若$p_{ij}+p_{ji}\geq\epsilon$，其中$\epsilon$是一个算术常数。

Sequence of chains. 看自闭了。。

Energy & power schedules. 让所有$s\in S^+$有一个能量。状态$i$的能量决定了应该由种子$t_i$变异生成的输入数量。一个状态的能量由预定义的power schedule决定。相当于FAIRFUZZ论文给出算法中的$score$。

Long tails. 固有分布中有很大数量的very-low-density regions和一小部分数量的very-high-density regions。

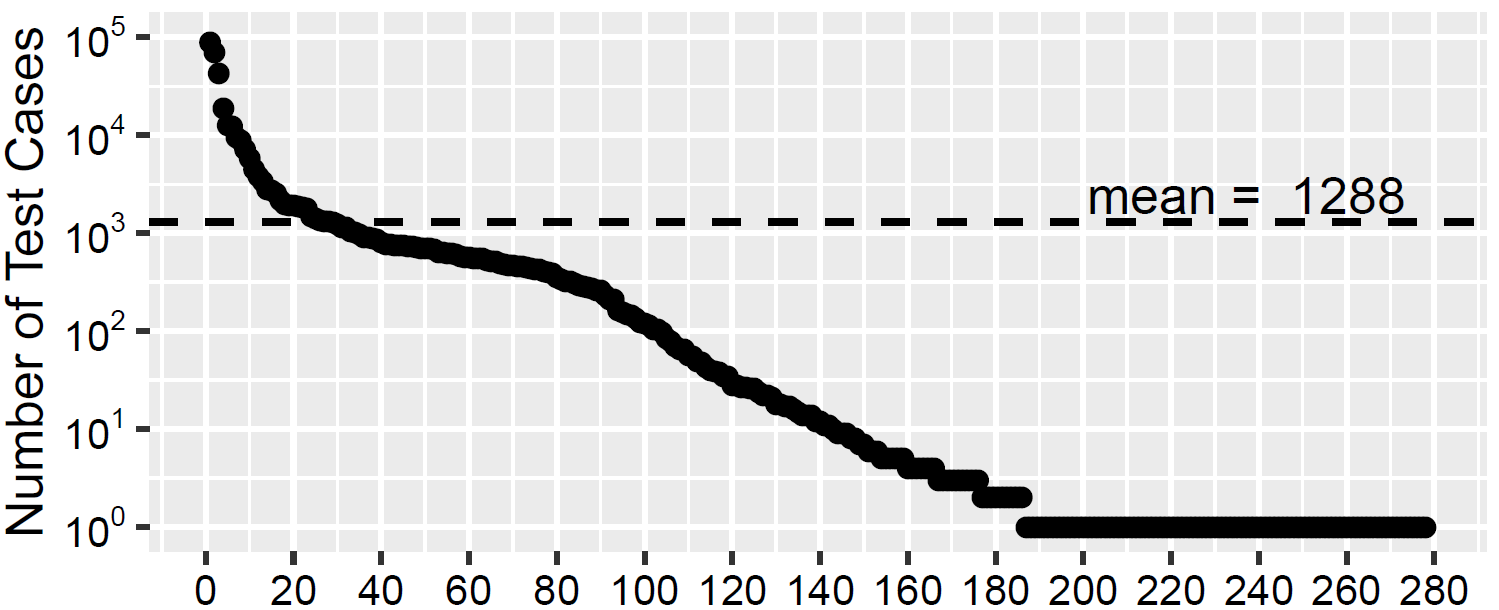
由图可知，大概30%的路径在简单的变异后就能执行到（185到280这一段），10%的路径需要生成1k到100k的测试用例后才能执行到（超过平均值的部分，0到30这一段）。也就是说，大多输入执行了少部分high-frequency paths。这些输入常常是不合法的。

Rapid mixing.

Benefits. 马尔科夫模型探索了程序的数值属性的有效近似，如最坏情况，平均执行时间和能量消耗。

3.2 运行实例

3.3 基于覆盖的Fuzzers的挑战

fuzzer通过CHOOSENEXT选择下一个输入$t\in T$，然后根据p=ASSIGNENERGY(t)决定生成变异输入的数量。通常$p\lt M,\ M\in \mathbb{N}$，M是变异生成输入的上界，在AFL中，$M\approx 160k$。

More Energy Than Needed. 设$i\in S^+$，$t_i$是执行状态$i$的种子输入。$X_{ij}$表示$t_i$通过变异发现新路径$j\in S^-$所需的变异次数，那么有以下式子：

$$\mathbb{E}[X_{ij}] = p_{ij}+(\mathbb{E}[X_{ij}+1])(1-p_{ij}) \\ \mathbb{E}[X_{ij}] = \frac{1}{p_{ij}}$$

Example.

设当$t_i$被选中时，状态$i$的能量为$p(i)=2^{16}=64k$。那么当从状态****的输入$t_0$变异了$2^{16}$次后，会有几个输入找到状态b***。

Excessive Energy for Hign-Density Regions. 若保留下来的输入执行high-density regions，会有一个趋势—会有太多的能量赋予这些状态。通过定义可知，若马尔科夫链中的状态$i$的固有分布密度越高，fuzzing $t_i$ 生成的输入会执行high-frequency paths。

Example. 栗子就不说了，主要抛出了两个挑战，AFL的power schedules：

1. 可能赋予过多的能量，超过了需求，给与新且有趣的路径
2. 可能赋予太多的能量给了high-density regions，给予low-density regions的能量不够

4 改进灰盒fuzzing

本文提出更有效的基于覆盖的灰盒测试fuzzers发现low-density region未发现的状态，同时分配最少的总能量。

1. Search Strategy. fuzzer选择$i\in S^+$，使得$\exists j\in S^-$另$\pi_j$is low且$\mathbb{E}[X_{ij}]$最小。
2. Power Schedule. fuzzer赋值的能量函数$p(i)=\mathbb{E}[X_{ij}]$给状态$i$，使得fuzzing发现low-density region时间达到最小

本文提出同构power schedules首先赋值低能量，然后根据选择的次数增加能量。同时，power schedules赋予状态的能量与状态固有分布的密度成反比。若状态$i$存在于low-density region，fuzzer可以分配更多能量来找这个区域中状态$i$的neighborhood。

4.1 Power Schedules

$s(i)$表示种子$t_i$之前从队列$T$中选到的次数。$f(i)$表示执行状态$i$的生成输入的数量。能量函数$p(i)$就是关于$s(i)$和$p(i)$的函数。$f(i)/n$是最大似然估计。接下来讨论几种power schedules：

exploitation-based constant schedule(EXPLOIT)：$p(i)=\alpha(i)$，其中$\alpha(i)$是算法中assignEnergy的实现。AFL根据执行时间，块转换覆盖率，$t_i$的构造时间来计算$\alpha(i)$。

exploration-based constant schedule(EXPLORE)：和EXPLOIT差不多$p(i)=\frac{\alpha (i)}{\beta}$，其中$\beta\gt 1$。

Cut-Off Exponential(COE)：

$$\begin{equation} p(i)=\left\{ \begin{array}{lcl} 0 && {\text{if}\ f(i)>\mu}\\ min(\frac{\alpha (i)}{\beta}\cdot 2^{s(i)}, M) && {\text{otherwise.}} \end{array} \right. \end{equation}$$

其中$\mu = \frac{\sum_{i\in S^+}f(i)}{|S^+|}$，也就是说说$\mu$是探索到的所有路径后生成数目数量的均值。

exponential schedule(FAST)：

$$p(i)=min(\frac{\alpha (i)}{\beta}\cdot \frac{2^{s(i)}}{f(i)}, M)$$

$s(i)$放在指数部分的直觉理由：本文提出的方法，期望的种子队列$T$本质上需要一个维护一个探索$low-density region$的输入序列，所以如果$s(i)$越大，直接含义上表示从输入队列中选择$t_i$输入的次数越多，也就是说状态$i$达到的路径数越少，状态$i$是个low-density region，所以放在指数上，$t_i$选取越多，就给它高能量值多变异变异。。。（太强大了，激动地说不出话_(:з」∠)_）

linear schedule(LINEAR)：

$$p(i) = min(\frac{\alpha(i)}{\beta}\cdot\frac{s(i)}{f(i)}, M)$$

quadratic schedule(QUAD)：

$$p(i) = min(\frac{\alpha(i)}{\beta}\cdot\frac{s(i)^2}{f(i)}, M)$$

4.2 Search Strategies

搜索策略下一个选啥种子，这个也hin重要。这个决策依赖于种子之前被fuzz过的次数和fuzz相同路径的种子的数量决定。本文认为一个好的基于灰盒测试的fuzzer应该给low-frequency paths高优先级。

小$s(i)$优先：$s(i)$表示种子$t_i$之前在队列中选到的次数。

小$f(i)$优先：$f(i)$表示执行状态为$i$的生成的输入的数量。

5 评价：VANILLA（香草？理解为原生的） VS BOOSTED CGF

5.1 实现：AFLFAST 1.94b

5.2 漏洞

这里要区别一下漏洞（vulnerability）和bug：https://yq.aliyun.com/ziliao/589078

大致意思就是bug一般指电脑系统的硬件或软件出错，漏洞一般指在软件，硬件，协议的具体实现或系统安全策略上存在缺陷（也就是说漏洞一般和安全相关？）

5.3 一般结果

5.4 Power Schedules比较

结果：AFLFAST中实现的的exponential schedule表现好于其他schedules。cut-off exponential schedule(coe)效果略差于AFLFAST。24小时的实验后，所有schedules发现的unique crashes比其他三种（linear，quad，explore）多50%。

5.5 搜索策略的比较

结果：两种策略的结合比各自使用策略效果更好。前12小时其他策略表现相似，24小时后策略1（改变了选favorite的策略）比策略2更有效。策略2（改变了从队列中选取测试输入的顺序）似乎效果不明显。用这个策略和不使用这个策略的AFLFAST效果相似。总之，AFLFAST集成两个策略后找到的unique crashes是原生AFLFAST或集成策略1找到unique crashes数量的2倍。

5.6 结果总结

在GUN binutils v2.26上评价了AFLFAST和几种搜索/调度策略。exponential schedule比其他schedules效果更好。8次6小时的执行中，以工具nm和c++filt作为benchmark，集成了exponential schedule的AFLFAST比AFL找到多找到了1个数量级的unique crashes。在8次24小时的运行中，AFLFAST6个nm中的漏洞，速度是AFL的7倍，并找到了3个AFL没有找到的漏洞。AFLFAST发现nm中的2个bug，速度是AFL的7倍，且找到了一个AFL没有找到的bug。平均来说，AFLFAST找error的速度是AFL的17倍，并且7个error是AFL没找到的。

6 基于符号执行的白盒fuzzing VS 基于覆盖的灰盒fuzzing

结论：在KLEE的benchmark bugs上进行评价比较

1. 在效率上，KLEE比AFLFAST好
2. 在效果上，1个小时的timeout内，AFLFAST的效果比KLEE好

为了检测漏洞，KLEE需要基于约束的漏洞检测机制和假设约束编码的完整性和环境建模，而AFLFAST仅仅需要执行程序报告任何crashes。

考虑代码覆盖率，AFLFAST比KLEE稍好。当然，结合起来使用效果更好，使用它们各自的强项来减弱对方的弱点。

7 在AFL 2.33B上部署

8 相关工作

9 结论

符号执行器的扩展性不如黑盒或灰盒的fuzzers。

本文提出一个方法改进AFL工具产生crash的效率。AFLFAST在单位时间内可以发现比AFL更多的unique crashes而且可以发现AFL不能发现的漏洞，其他的漏洞AFLFAST发现的比AFL早。

更重要的是，本文提供了通过把CGF建模为Markov chain探索状态空间的尝试。本文的方法会尝试隐藏在low-density region上更多的状态和在high-density region上生成更少的输入。

一篇paper看两天。。