一 递归函数
1.1 数论函数（P1）
本源函数$\mathcal{IF}$：
- 零函数Z
- 后继函数S
- 投影函数$P^n_i$
1.2 配对函数（P7）
配对函数：设$pg(x,y):\mathbb{N}^2\rightarrow\mathbb{N}, K(x):\mathbb{N}\rightarrow\mathbb{N}, L(x):\mathbb{N}\rightarrow\mathbb{N}$为数论函数，若它们对于任意$x, y\in\mathbb{N}$，满足：$K(pg(x,y))=x, L(pg(x,y))=y$，则称$pg$为配对函数，$K$和$L$分别为左函数和右函数，$\{pg, K, L\}$为配对函数组。
1.3 初等函数（P14）
初等函数$\mathcal{EF}$：
- $\mathcal{IF}\subset\mathcal{EF}$
- $x+y, x-y, x\times y, \lfloor x/y\rfloor\in\mathcal{EF}$
- $\mathcal{EF}$对于复合，有界叠加算子$\sum[\cdot]$和有界迭乘算子$\prod[\cdot]$封闭
- $x\times y, N(x), N^2(x)$
- $\mathcal{EF}$对于$\mu-$算子和$max-$算子封闭
- $x^y, \sqrt[y]{x}, rs(x,y)$
- $\tau(x)$：$x$的因子的数目
- $prime(x)$：判断$x$是否为素数
- $\pi(x)$：不超过$x$的素数个数
- $P(n)$：枚举第n个素数
- $ep(n, x)$：$x$的素因子分解式中$P_n$的指数
1.4 原始递归函数（P25）
（P25）原始递归函数：类$\mathcal{PRF}$是满足一下条件的最小集合：（1）$\mathcal{IF}\subseteq\mathcal{PRF}$ （2）$\mathcal{PRF}$对于复合，带参原始递归算子和无参原始递归算子封闭。
原始递归函数（$\mathcal{PRF}$）：
- $add(x, y)$
- $pred(x, y)$
- $sub(x, y)$
- $diff(x, y)$
- $mul(x, y)$
- $sq(x)$
- $N(x)$
- $N^2(x)$
- $sqrt(x)=\lfloor\sqrt{x}\rfloor$
- $E(x)=x-\lfloor\sqrt{x}\rfloor^2$
（P30）原始复迭函数类（$\mathcal{IIF}$）：（1）$\mathcal{IF}\subseteq\mathcal{IIF}$（2）$\mathcal{IIF}$对于复合、原始复迭算子$It[\cdot]$、弱原始复迭算子$Itw[\cdot]$封闭。
（P32）定理1.47：$\mathcal{IIF}=\mathcal{PRF}$
（P33）串值递归
（P34）联立递归、变参递归
（P35）多重递归
（P36）Ackermann函数
1.5 递归函数（P40）
正则函数、正则$\mu-$算子、$\mu-$算子、一般递归函数（$\mathcal{GRF}$）、部分递归函数（$\mathcal{RF}$）
1.6 不可计算数论函数类
- （P102）集合$\mathcal{N}=\{M:M$有$\beta-nf\}$
- （P100，P102）在$\lambda-$演算中，等价关系$=_\beta$是不可判定的（存在$M, N\in \Lambda$使得$m=\lceil M\rceil, n=\lceil N\rceil$且$M=_\beta N$）
- （P136）停机问题：存在Turing机使$n=\sharp M$且$M$对于一切输入皆停机
1.7 第二大题分类情况
- $\mathcal{EF}$：1. 向下取整类型 2. Godel的$\beta-$函数 3. $\pi$的十进制展开中的第$n$个数字 4. $e$的十进制展开中的第$n$个数字（hint：1. $\pi/4=1-1/3+1/5-1/7+\dots$ 2. $e=\sum_{i=0}^{n}(1/i!)$）
- $\mathcal{PRF-EF}$：1. 类似$G(x)=2^{2^{2^{\dots^{x}}}}$
- $\mathcal{GRF-PRF}$：1. Ackermann函数
- $\mathcal{RF}-\mathcal{GRF}$：1. $f:\mathbb{N}\rightarrow\mathbb{N}$为处处无定义的函数 2. 存在无定义的函数（P40 $\mu-$算子定义）
- 不可计算数论函数类：见1.6
三 $\lambda-$演算
3.1 $\lambda-$演算的语法（P70）
约定3.3 ：
- $x,y,z$表示任意变元
- $M,N,L$表示任意$\lambda-$项
- $M\equiv N$表示M和N语法恒同
- 通常采用以下省略括号表示法
- 左结合：$FM_1M_2\dots M_n\equiv(\dots((FM_1)M_2)\dots M_n)$
- $\lambda x_1 x_2\dots x_n.M\equiv(\lambda x_1(\lambda x_2(\dots(\lambda x_nM)\dots)))$
- 设$P\equiv MN_1\dots N_k$，其中$k\geq 0$，当$k=0$时，$P\equiv M$
- 设$P\equiv \lambda x_1\dots x_n.M$，其中$k\geq 0$，当$k=0$时，$P\equiv M$
3.2 转换（P74）
形式理论$\lambda\beta$由以下的公理和规则组成：
公理：
- $(\rho)M=M$
- $(\beta)(\lambda x.M)N=M[x:=N]$
规则：
- $(\sigma)\frac{M=N}{N=M}$
- $(\tau)\frac{M=N, N=L}{M=L}$
- $(\mu)\frac{M=N}{ZM=ZN}$
- $(\nu)\frac{M=N}{MZ=NZ}$
- $(\xi)\frac{M=N}{\lambda x.M=\lambda x.N}$
（P76）标准组合子：
- $I\equiv\lambda x.x$
- $K\equiv\lambda xy.x$
- $K^*\equiv\lambda xy.y$
- $S\equiv\lambda xyz.xz(yz)$
（P76）定义3.14
- 形式理论$\lambda\beta+ext$是在形式理论$\lambda\beta$中加入下述规则(ext)：$(ext) Mx=Nx\Rightarrow M=N$，其中$x\notin FV(MN)$
- 形式理论$\lambda\beta\eta$是在形式理论$\lambda\beta$中加入下述公理$(\eta)$：$(\eta)\lambda x.Mx=M$，其中$x\notin FV(M)$
3.3 规约（P77）
| 关系 | 性质 | 读法 | 备注 |
|---|---|---|---|
| $\rightarrow_R$ | 合拍 | 一步$R-$规约 | R的合拍闭包 |
| $\twoheadrightarrow_R$ | 规约 | $R-$规约 | $\rightarrow_R$的自反、传递闭包 |
| $=_R$ | 同余 | $R-$转换 | $\twoheadrightarrow_R$的对称闭包 |
$\beta-nf$：
- $(\lambda x.xx)y$不是$\beta-nf$，但$yy$是它的$\beta-nf$
- $\Omega\equiv (\lambda x.xx)(\lambda x.xx)$不是$\beta-nf$，也无$\beta-nf$
- $(\lambda u. v)\Omega$不是$\beta-nf$，但它有$\beta-nf$，而且有无穷$\beta-$化归链
3.5 不动点定理（P91）
（P91）定理3.22（不动点）定理：对于任意的$F\in\Lambda$，存在$Z\in\Lambda$，使得$FZ=_\beta Z$。
3.6 递归函数的$\lambda-$可定义性（P93）
（P93）Church数项：对于$n\in \mathbb{N}$，Church数项$\lceil n\rceil$定义为$\lceil n\rceil\equiv\lambda fx.f^nx$
$\lambda-$可定义函数类：
- 一般递归函数式$\lambda-$可定义的
- 本源函数
- 对复合封闭，对原始递归封闭
部分$\lambda-$定义函数：
- 本源函数
- 后继函数$S$
- 前驱函数$PRED$
- 选择函数$D$
$D\lceil 0\rceil=_\beta U_1^2,\ D\lceil n+1\rceil=_\beta U_2^2$，因此$D\lceil 0\rceil MN=_\beta M,\ D\lceil n+1\rceil MN=_\beta N$
3.7 与递归论对应的结果（P98）
（P99）定理3.42 第二不动点定理：$\forall F. \exists Z.F\lceil Z\rceil=_\beta Z$
3.8 第三大题套路
一般是对给定的数论函数$f(x)$，构造$F\in \Lambda^\circ$其$\lambda-$定义$f(x)$。
做题套路：
- 首先将$f(x)$写成原始复迭式/弱原始复迭式形式$f(0)=a, f(x+1)=g(f(x))$
- 可知$f(x)=g^n(a)$，那么$F\lceil x\rceil=_\beta\lceil g^n(a)\rceil=_\beta G^n\lceil a\rceil\equiv\lceil n\rceil G\lceil a\rceil\equiv(\lambda x.xG\lceil a\rceil)\lceil n\rceil$
- 构造$G\lceil x\rceil$使其$\lambda-$定义$g(x)$
$\square$
3.9 第四大题套路
在已有的公理系统中加入一个额外公理$(*)$，使用规则和标准组合子推出对任何$M,N\in\Lambda$，$\lambda\beta + (*)\vdash M=N$。
- 套路1：$(*)\lambda x.x=\lambda x.xx$，对于接收一个参数的，一般参数代入$K$，然后添加$M$，得到$M=$标准组合子复合，$N$同理，得到$M=N$。
- 套路2：$(*)\lambda xy.xy=\lambda xy.yx$，对于接收两个参数的，一般参数代入$KI$，然后添加$MN$，得到$M=N$。
- 2004年题：$(*)x(yz)=(xy)z,\lambda\beta+(*)\vdash M=N$。$KII$代入两边得到$K(II)\equiv KII\Rightarrow KI=I$，两边加$M$得到$KIM=IM\Rightarrow I=M$，同理$I=N$，那么有$M=N$。
五 Turing机
5.1 Turing机的形式描述（P119）
（P120）定义5.1（Turing机）：设$D\subset\{0,1\}\times \mathbb{N}^*$为有穷集，函数$d:D\rightarrow\{0,1\}$，$p:D\rightarrow\{-1,0,1\}$，$s:D\rightarrow\mathbb{N}^*$。三元组$(d,p,s)$被称为一个Turing机，记作$M=(d,p,s)$。称集合$D$为$M$的论域$Dom(M)$，函数$d$为$M$的“印-抹”函数，函数$p$为$M$的位置函数，函数$s$为$M$的状态函数。
（P122）定义5.6（Turing-可计算）：设$M$为机器，$f:\mathbb{N}^n\rightarrow\mathbb{N}$为$n$元数论全函数。若对于任意$(x_1, x_2, \dots. x_n)\in \mathbb{N}^n$，$M$输入$\overline{\mathop{(x_1, \dots, x_n)}}$可输出$\overline{f(x_1, \dots, x_n)}$，则称机器$M$计算了函数$f$。当存在机器$M$计算函数$f$时，称函数$f$为Turing-可计算。
5.2 Turing机的计算能力（P125）
（P126）引理5.4：设$f:\mathbb{N}\rightarrow\mathbb{N}$，$g:\mathbb{N}^k\rightarrow\mathbb{N}$，若$f,g$皆为Turing-可计算，则$h(\mathbf{x})=f(g(\mathbf{x}))$为Turing-可计算。
已有的机器：
copy_k：拷贝当前所指的值compress：将$0^n$压缩到$0$erase：抹去当前值shiftlshiftrdouble
5.3 可判定性与停机问题（P136）
（P139）停机问题：是否存在能行过程（effective procedure）来判定机器对所有输入皆停机。
回答：答案是否定的，即停机问题不可判定。
5.4 通用Turing机（P139）
问题：什么是通用Turing机？
回答：（P144）存在机器$U$使对任何机器$M$和任何$(n_1, n_2, \dots, n_k)\in n^k, M|\overline{(n_1, n_2, \dots, n_k)}\twoheadrightarrow\overline{y}\Leftrightarrow U|\overline{(\sharp M, n_1, \dots, n_k)}\twoheadrightarrow\overline{y}$
则称机器$U$为通用Turing机，通用性是指这样的机器能模拟任何其他Turing机。
5.5 Church-Turing论题（P145）
定理5.29（基本定理）：目前已知的各种刻画能行可计算的模型给出了相同的可计算函数类。
Church-Turing论题：直觉能行可计算（部分）函数类等同于Turing-可计算（部分）函数类。
总之，计算概念的可视化是20世纪的重大科学进展之一。
5.6 停机问题叙述套路
对于给定的一个机器$M$，设计机器$Evil$，当$Evil$检测到$M$判断为停机时，则保持不停机；否则停机，得出矛盾。
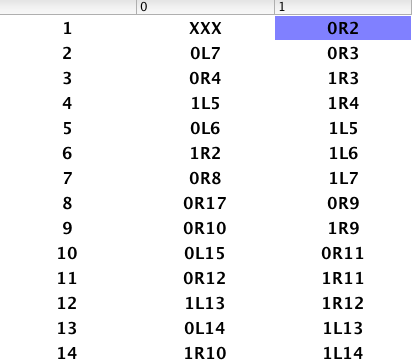
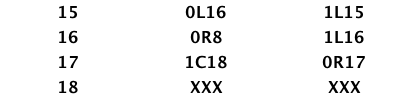
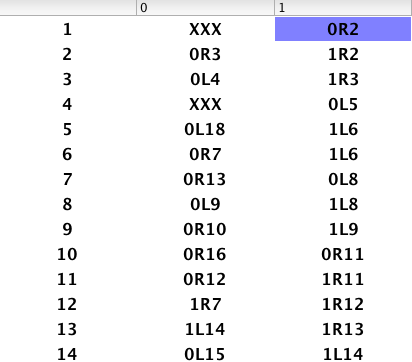
5.7 一些常用图灵机
- $f(x)=2x$
1.去掉一根棍子 2-5.copy16.中间连起来
1.去掉一根棍子 2-7.去掉一根，加上两根
1-8.去掉一根棍子，加上两根棍子 9.去掉一根棍子
- 棍子数*2
- $f=3x$
1.去掉一根棍子 2-7.去掉一根棍子，加两根棍子，中间连起来
copy_1（习题5.2）- $f(x)=\lfloor x/2\rfloor$
1.去掉一根 2-7.每去掉两根，加一根
1-3.头里去一根，尾巴上去一根 4-5.最前面加一根
1-6.去掉两根棍子，加一根棍子
$f(x)=\lfloor x/3\rfloor$
1-6. 前面去1根棍子，后面去3根棍子，最前面加1根棍子
- $f(x)=x-y$（习题5.11）
- $f(x, y)=xy$（习题5.3）
1-7. x减一根，y减一根 8-15.复制一份y 16.加一根
- $f(x)=x^2$
- $f(x)=\lfloor x^{\frac{1}{2}}\rfloor$
- $f(x)=x/y$
